[Selection/Exchange Sort] 선택정렬ㆍ교환정렬

[Bubble Sort]

[Selection Sort] 선택정렬

가장 정상적인? 정렬방식이다. 가장 인간 친화적인 알고리즘이라고 생각한다.

우리가 트럼프카드를 정리하는 경우를 생각해보자. 카드들이 무작위적으로 마구 섞여있는데, 우리는 편의상 클로버2부터 클로버10까지만 존재한다고 치자. 참고로 우리나라와 프랑스는 ♧를 클로버라고 부르고, 일본과 미국은 클럽이라고 부른다고 한다.

다시 돌아와서, 당신이라면 어떻게 정리할 계획인가?

필자라면 10번부터 2번까지 차례대로 찾아서, 10-9-8-7-…-2 순서대로 아래서부터 차곡차곡 쌓을 것 같다. 사실 꽤나 쉬운 작업이다. 우리 눈은 가장 먼저 10을 찾을테고, 그 다음은 당연히 9, 다음은 당연히 8을 찾을테니 말이다.

그런데 2~10 아홉장의 카드 중 몇장이 빠져 있다면 어떨까? 1, 4, 6, 9, 10이 빠지면 2, 3, 5, 7, 8만 남는다. 이 다섯장을 정렬한다고 생각해보자. 이 때는 무슨 기준으로 맨 아래 쌓을 카드를 찾을 것인가?

다섯장의 카드 중 가장 큰 숫자의 카드를 찾으면 된다! 별로 놀랍지도 않은 지루한 내용이라 놀라운 척을 한 번 해봤다.. 아무튼 우리가 찾은 카드는 8이다.

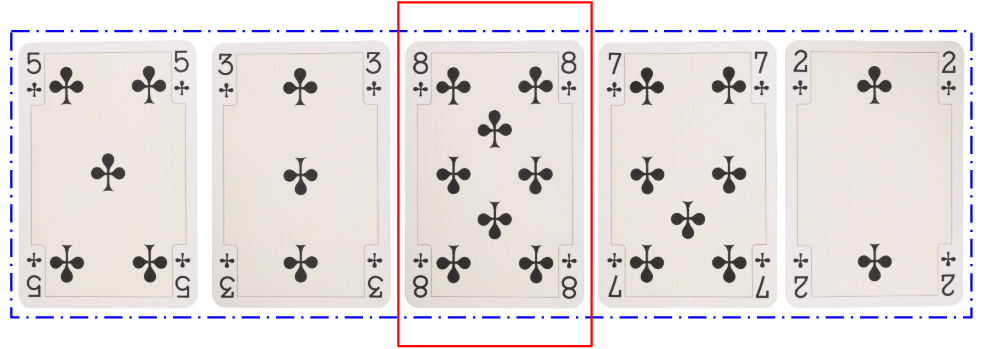
그 카드를 맨 아래에 깐 다음(여기서는 맨 뒤로 보낸다. 맨뒤의 카드와 순서를 바꿀 것이다. 한칸씩 앞으로 당기지 않는 이유는? 카드를 옮겨야 하는 횟수를 생각해보자. 바꾸는 경우가 훨씬 적다.), 이제 남은 카드 중에서 그 다음으로 큰 숫자를 찾는다.

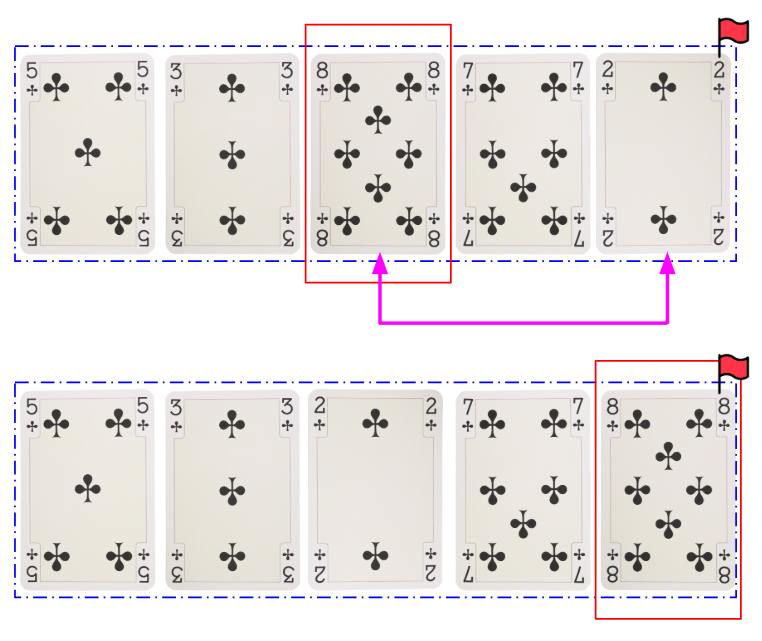
즉, 맨 뒷자리부터 자리의 주인을 찾아주면서, 맨 앞 장의 카드 하나가 남을 때까지 이를 반복하면 된다.

그림으로 나타내보자.

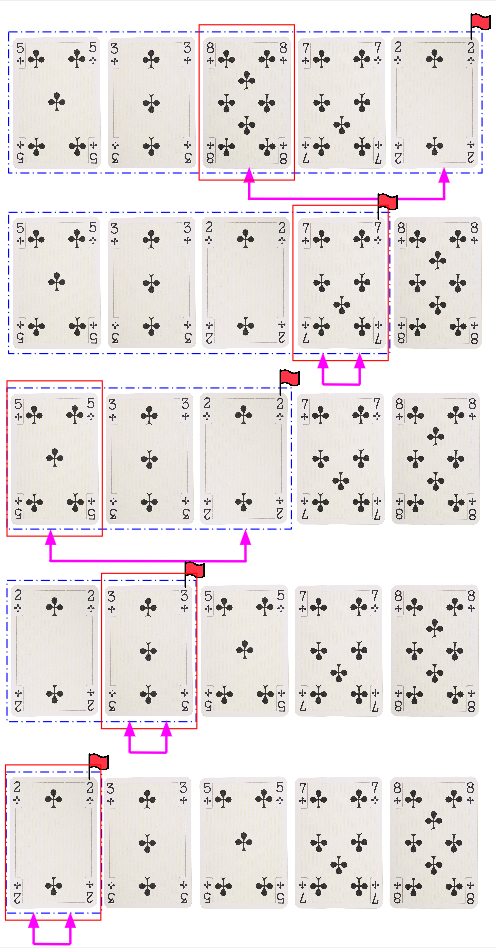
이제 카드가 잘 정렬 된 모습을 볼 수 있다. 상기 알고리즘을 코드로 구현하면 이하와 같다.

# Selection Sort
arr=[5,3,8,7,2]
print(arr)
### 선택정렬 시작! ###
for flag in range(len(arr)-1,0,-1):  #flag=내가 현재 값을 확정해주고 싶은 위치
    maxVal= arr[flag]                #일단 [flag 위치의 값]이 가장 크다고 가정
    maxIdx= flag
    for tmp in range(0,flag,+1):     #당연히 0부터 (flag-1)까지의 값을 [flag 위치의 값]과 비교해본다
        if (arr[tmp]>maxVal):        #그러다 flag보다 큰 값이 나올 경우 기억해둔다
            maxVal= arr[tmp]
            maxIdx= tmp
    arr[maxIdx],arr[flag]=arr[flag],arr[maxIdx] #[flag 위치의 값]과 [0부터 flag까지 중 가장 큰 값을 교환한다]
print(arr)

여기서부터는 몇가지 평범하지 않은 사람들이 선택정렬을 자기만의 방식으로 활용해 사용하는 방법이다.

성격 급한 도널드의 [Exchange Sort] 교환정렬

선택정렬을 수행하던 도널드는 매번 가장 큰 카드를 찾고 나서 더 큰 수가 없는지 확인하는 과정이 지겨워졌다. 그래서 [flag 위치의 값]보다 큰 카드를 앞에서 찾자마자 바로 [flag 위치의 값]과 바꾸어버리기로 마음먹었다. 마음대로 규칙을 바꿔 정렬을 수행한 도널드.. 당연히 카드뭉치가 엉망진창이 될 줄 알았으나..! 도널드가 맨 앞장 한 장을 남겨두었을 때, 정렬은 정상적으로 이루어졌다!

사실 도널드의 방식도 상관이 없는 것이, 가장 큰 수가 수열 어디엔가 존재할 것이기 때문에, 계속해서 바꾸더라도 결국엔 맨 뒤로 오기 때문이다. 물론, 도널드가 조금 더 수고는 하겠지만 말이다.

선택정렬을 수행할 때, 우리는 [첫번째 값]부터 [flag 위치의 값]까지 모두 살피고 그 중 가장 큰 값을 [flag]에 옮겼다.

그러나 교환정렬을 수행할 때에는 [첫번째 값]부터 [flag 위치의 값]까지 살피는 도중 [tmp 위치의 값]이 [flag 위치의 값]보다 크다면 고민도 하지 않고 가차없이! 바로 바꿔버린다.

위의 코드를 바탕으로 새로 구현해보면 다음과 같다.

# Exchange Sort
arr=[5,3,8,7,2]
print(arr)
### 교환정렬 시작! ###
for flag in range(len(arr)-1,0,-1):  #flag=내가 현재 값을 확정해주고 싶은 위치
    for tmp in range(0,flag,+1):     #당연히 0부터 (flag-1)까지의 값을 [flag 위치의 값]과 비교해본다
        if( arr[tmp]>arr[flag] ):    #그러다 [tmp 위치의 값]이 [flag 위치의 값]보다 크면 냅다 바꾼다.
            arr[tmp],arr[flag]=arr[flag],arr[tmp]
print(arr)

키가 짧아 슬픈 하미드의 [Gnome Sort] 난쟁이정렬

한편, 우리 하미드(Gnome Sort의 개발자는 실제로 Hamid Sabrazi-Azad라고 알려져있다. 그는 난쟁이가 화분을 옮기는 모습을 보며 해당 정렬을 고안한 것으로 알진 바 있다.)는 릴리펏 왕국(The Lilliput, 걸리버 여행기에 나오는 신장 약 15cm의 소인국)의 주민이다. 우리에겐 손바닥만한 트럼프 카드가 하미드에게는 무지막지한 짐이다. 그래서 하미드는 거리가 멀리 떨어진 카드의 위치를 한번에 바꾸는 것이 어렵다 ㅠㅠ

그래서 하미드는 꼼수를 생각해냈다. 항상 붙어있는 두개의 숫자끼리만 크기를 비교하는 것이다. 하미드는 이렇게 하면 자신이 총총총 이동하면서 가장 큰 카드를 맨 뒤로 가져올 수 있을 거라고 생각했다.

하지만 정말 그래도 될까? 그럴리가!

세상은 도널드처럼 열심히 하는 사람들에게는 관대하지만, 하미드처럼 잔머리를 굴리는 사람들에게는 가혹한 법이다. 불쌍해. 작게 태어난 것도 서러운데

하미드는 두번째 카드를 옮기자마자 뭔가 잘못되었다는 걸 느꼈다.

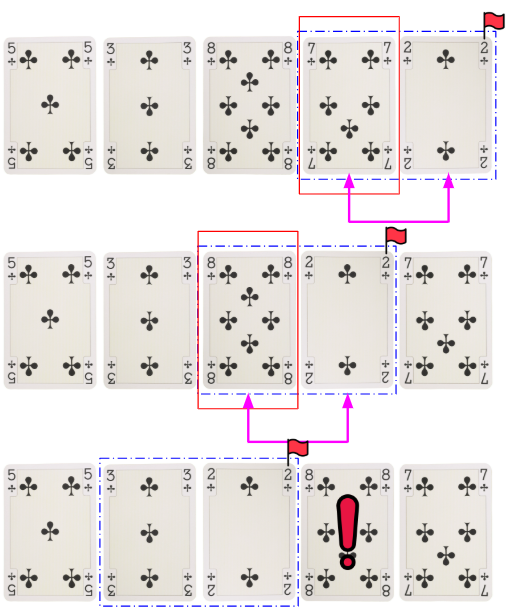
하미드는 이미 맨 뒷자리에 7을 박아두었지만, 그것보다 더 큰 8 카드가 등장해버린 것이다! 그렇다. 그는 두개씩 교환할 때, 이미 정렬해둔 자리에 가야하는 더 큰 숫자가 올 수 있다는 것을 간과하고 있었다.

그래서 하미드는 자신의 알고리즘에 조그마한 수정을 가하기로 했다.

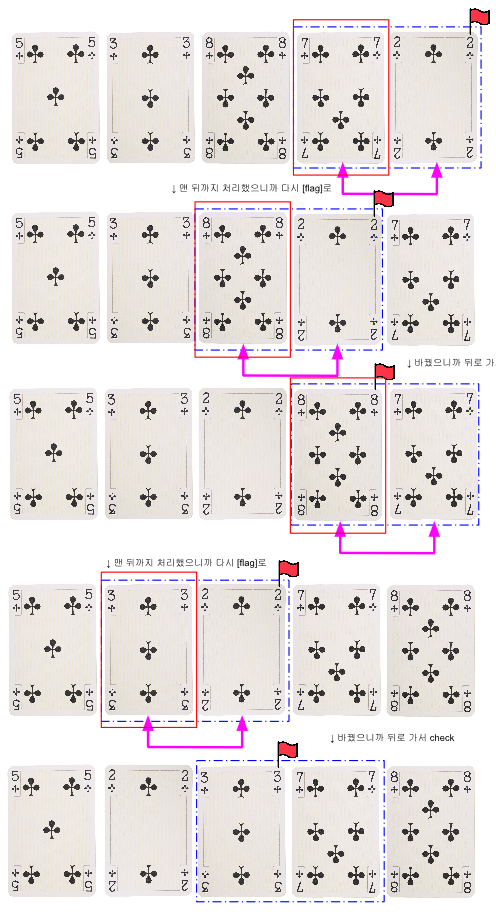
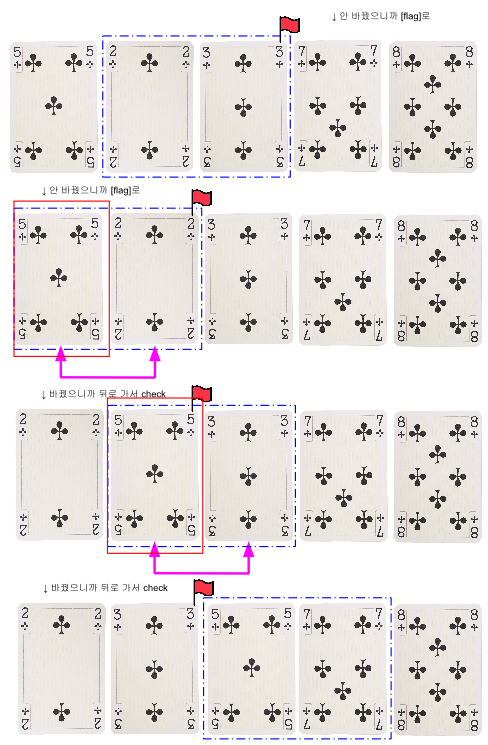
파란 네모 박스 안에서 두개씩의 카드를 비교하되, [앞 카드 숫자]가 [뒷 카드 숫자]보다 작아서 교환을 하지 않은 경우는 그냥 넘어가지만, 순서를 바꿔야할 필요가 있는 큰 [앞 카드 숫자]가 등장하는 경우에는 자신이 이미 정렬해두었던 flag 뒤로 이동하며 [앞 카드 숫자]의 위치를 다시 찾아주기로 했다. 하마드는 아직 자신이 까지 않은 카드들을 제외하면 항상 최선을 다하고 있는 셈이다..!

이제 하미드의 알고리즘이 잘 작동하는지 다시 한번 같이 살펴보자.

# Gnome Sort
arr=[5,3,8,7,2]
print(arr)
### 난쟁이정렬 시작! ###
for flag in range(len(arr)-1,0,-1):   #flag=내가 현재 값을 확정해주고 싶은 위치
    whereIsHamid = flag               #하미드는 flag로부터 스스로 총총 움직이며 카드를 한쌍씩 swap한다
    while ( whereIsHamid<len(arr) and arr[whereIsHamid-1]>arr[whereIsHamid]):         #한쌍의 순서에 문제가 있을 때!
        arr[whereIsHamid-1],arr[whereIsHamid] = arr[whereIsHamid],arr[whereIsHamid-1] #바꾼다 하미드
        whereIsHamid = whereIsHamid+1
print(arr)

정리하자면, 위의 모든 알고리즘은 Selection Sorting의 다양한 형태이다. Selection Sorting의 특징은

1. flag를 정하여
2. flag에 위치해야할 element를 찾고
3. 해당 element를 flag의 위치로 이동

한다는 점이다. 우리는 일관성을 잃지 않고 WLOG 항상 flag를 뒤에서부터 잡아왔다.(1) 앞에서부터 세우든, 오름차순이 아닌 내림차순으로 세우든 모든 원리는 동일하다.

일반적인 Selection Sort는 flag를 기준(1)으로 순차탐색 linear search을 통해 maximum element를 특정(2)하고, 한번에 index 기준 swap을 수행(3)한다.

하지만 Exchange Sort는 flag를 기준(1)으로 순차탐색 linear search을 통해 maximum element를 특정(2)하고 매번 index 기준 swap을 수행(3)한다.

마지막으로 Gnome Sort는 flag를 기준으로 부분탐색 partial search를 통해 local maximum element를 특정(2)하고 단순 swap을 수행(3)해 absolute maximum을 특정한다.